Introduction to Markov chains

Table of Content

What is a markov chain

A Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). It is named after the Russian mathematician Andrei Markov (1856-1922), who introduced it in 1906.

These statistical models have a large number of real applications.

Where are Markov chain used?

Markov chains have experienced an important real-world application in the field of business and finance. This, by allowing, as has been pointed out, to analyze and estimate future behavior patterns of individuals based on experience and previous results.

This can be reflected in different fields such as delinquency, the study of consumer behavior, seasonal demand for labor, among others.

The system elaborated by Markov is quite simple and has, as we have said, a fairly easy practical application. However, many critical voices point out that such a simplified model cannot be fully effective in complex processes.

Markov chain by example

Imagine that there were two possible states for weather: sunny or cloudy. You can always directly observe the current weather state, and it is guaranteed to always be one of the two aforementioned states.

Now, you decide you want to be able to predict what the weather will be like tomorrow. Intuitively, you assume that there is an inherent transition in this process, in that the current weather has some bearing on what the next day’s weather will be. So, being the dedicated person that you are, you collect weather data over several years, and calculate that the chance of a sunny day occurring after a cloudy day is 0.25. You also note that, by extension, the chance of a cloudy day occurring after a cloudy day must be 0.75, since there are only two possible states.

You can now use this distribution to predict weather for days to come, based on what the current weather state is at the time.

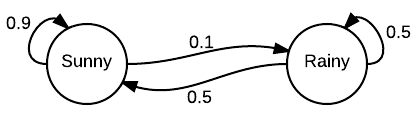
A visualization of the weather example Markov Chain.

Other Markov Chain use cases

Meteorology

If we consider the weather in a region over different days, it is possible to assume that the current state depends only on the last state and not on the whole history itself, so that Markov chains can be used to formulate basic climatological models. For example, rainfall recurrence models based on Markov chains have been developed.

Epidemiological models

An important application of Markov chains is in the Galton-Watson process. This is a branching process that can be used, among other things, to model the development of an epidemic (see mathematical modeling of epidemics)

Internet

The pagerank of a web page (used by Google in its search engines) is defined through a Markov chain, where the position that a page will have in the search engine will be determined by its weight in the stationary distribution of the chain.

Simulation

Markov chains are used to provide an analytical solution to certain simulation problems, for example in queueing theory the M/M/1 Model is in fact a Markov chain model.

Games of chance

Many games of chance can be modeled by means of a Markov chain. The Gambler’s ruin model, which establishes the probability that a person who bets on a game of chance will eventually end up out of money, is one of the applications of Markov chains in this area.

Economics and finance

Markov chains can be used in simple option valuation models to determine when there is an arbitrage opportunity, as well as in modeling stock market crashes or determining price volatility. In business, Markov chains have been used to analyze the buying patterns of delinquent debtors, to plan staffing needs, and to analyze equipment replacement.

Genetics

Markov chains are used in population genetics theory to describe the change in gene frequencies in a small population with discrete generations subject to genetic drift. It has been used in the construction of Motō Kimura’s diffusion model.

Music

Several music composition algorithms use Markov chains, for example Csound or Max software. One of the composers who used this technique in his compositions was Iannis Xenakis with his work Analoguique A et B (1958-59).

Operations

Markov chains are used in inventory, maintenance and process flow.

Neural networks

They are used in Boltzmann machines.

Modelling a Markov chain

Markov chains may be modeled by finite state machines, and random walks provide a prolific example of their usefulness in mathematics. They arise broadly in statistical and information-theoretical contexts and are widely employed in economics, game theory, queueing (communication) theory, genetics, and finance.

Formally, a Markov chain is a probabilistic automaton. The probability distribution of state transitions is typically represented as the Markov chain’s transition matrix. If the Markov chain has $N$ possible states, the matrix will be an $N x N$ matrix, such that entry $(i, j)$ is the probability of transitioning from state $i$ to state $j$. Additionally, the transition matrix must be a stochastic matrix, a matrix whose entries in each row must add up to exactly $1$. This makes complete sense, since each row represents its own probability distribution.

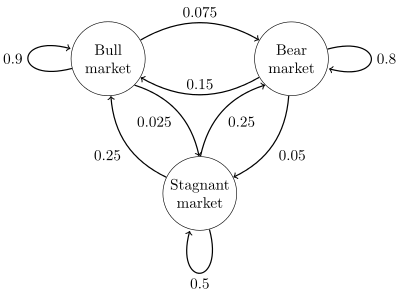
General view of a sample Markov chain, with states as circles, and transitions as edges.

Previous chain visual representation, can also be described as following matrix

$$ P = \begin{bmatrix} 0.9 & 0.075 & 0.025 \newline 0.15 & 0.8 & 0.05 \newline 0.25 & 0.25 & 0.5 \end{bmatrix} $$

We now know how to obtain the chance of transitioning from one state to another, but how about finding the chance of that transition occurring over multiple steps? To formalize this, we now want to determine the probability of moving from state $i$ to state $j$ over $m$ steps. As it turns out, this is actually very simple to find out. Given a transition matrix $P$ this can be determined by calculating the value of entry $(i, j)$ of the matrix obtained by raising $P$ to the power of $M$. For small values of $M$, this can easily be done by hand with repeated multiplication. However, for large values of $M$, if you are familiar with simple Linear Algebra, a more efficient way to raise a matrix to a power is to first diagonalize the matrix.

Continue reading

You can continue reading more post about markov chains:

Part 1: Introduction to markov chain
Part 2: How to build a markov chain with Python
Part 3: How to build a markov chain with Go

References

Subscribe, donate or become premium

Thanks for checking this out and I hope you found the info useful! If you have any questions, don't hesitate to write me a comment below. And remember that if you like to see more content on, just let me know it and share this post with your colleges, co-workers, FFF, etc.